Contents
重回帰分析：Multiple Regression
重回帰分析(Multiple regression)はLevel IIのQuantitative Methodsの中心になります。EquityやPortfolio Managementの項目でもその概念が利用されていて、ここで正しく重回帰分析を学んでおくと理解が進みます。
t検定やF検定、ANOVA Tableの考え方は単回帰分析と同様です。HeteroskedasticityやSerial correlation、Multicollinearityなど、重回帰分析がうまく行かないケースについてちゃんと見ておきましょう！
重回帰分析（Multiple Regression）の導入
単回帰分析は二つの事象の当てはまりが良い一次関数の直線（変数が一つ）を探しましたが、重回帰分析では変数が複数の数式で表現することになります。具体的な数式例は以下をご覧ください。
\(Y_i = b_0 + b_1X_{1i} + b_2X_{2i} + … + b_kX_{ki} + ε_i\)
\(Y_i\)は従属変数(i=1〜n: nは標本数)
\(X_1〜X_{ki}\)は独立変数(\(k\)は独立変数の数)
\(b_0\)はIntercept
\(b_j\)は独立変数のslope
\(ε\)は誤差項(独立した変数であり、平均ゼロの正規分布に従う)
単回帰分析とは違って若干複雑な式になっていますが、単純に変数が増えただけですので焦る必要は全くありません。t値の出し方も検定の仕方も単回帰分析の場合と特に変わりは無いです。ANOVA Tableも単回帰分析で見たものと同様になります。
ダミー変数（Dummy Variables）
重回帰式のうち、変数が0か1を取るものをダミー変数を用いた回帰分析と言います。
例えば、以下のような四半期毎にとある数値を求める数式です。
\(Y = b_0 + b_1Q_1 + b_2Q_2 + b_3Q_3 + ε\)
この場合、第一四半期の時は\(Q_1=1\)、第二四半期の時は\(Q_2=1\)、第三四半期の時は\(Q_3=1\)として、それ以外の時は0の値をとります。こうして四半期毎の数値を表現する数式にしているわけですね。こういったものをダミー変数を用いた数式と言います。
ここからは、重回帰分析がうまく行かないケースについて眺めておきましょう！
ポイントは、うまくいかないケースの名称と意味の確認。どのようにそれら事象を発見するか。発見したらどのように修正するか。になります。それでは見て行きましょう！
不均一分散(Heteroskedasticity）
不均一分散とは
標本データの誤差項の分散が均一で無い状態を指します。回帰分析では誤差項εは期待値がゼロで分散が一定という前提を置いているため、誤差項の分散が均一で無いと問題になります。
不均一分散には、独立変数の数値に関係無く誤差項がバラバラに散布するUnconditional heteroskeasticityと、独立変数の数値が増加するに連れて誤差項が大きくなる、Conditional heteroskedasticityがありますが、後者については正しいモデル結果を算出するためには直す必要があると言われています。
以下のグラフは問題となるConditional heteroskedasticityの例です。Xが大きくなるほど誤差項が大きくなっているのが分かるかと思います。
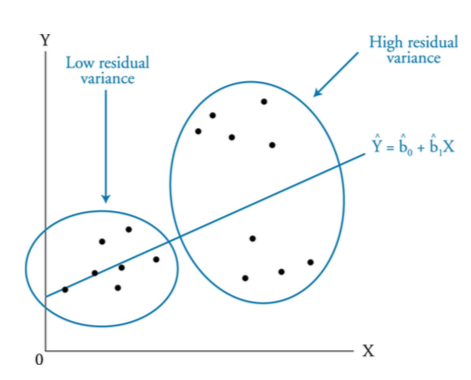出所：Schweser Notes不均一分散の発見方法
不均一分散を発見するためには2つ方法があります。一つは以下のグラフのように実際に誤差項を図にプロットして確認する方法です。
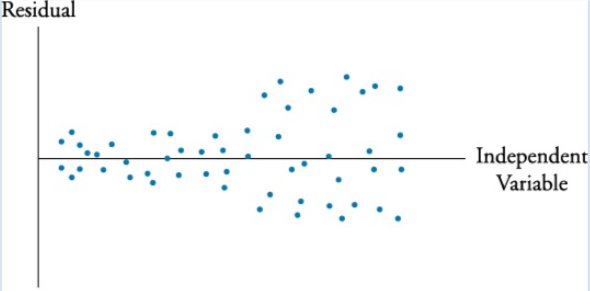出所：Schweser Notes
もう一つが、The Breusch-Pagan Testと呼ばれるテストを行うことです。
ここでは詳細は省略しますが、Heteroskedasticityを検知するためにはThe Breusch-Pagon Testを用いるということを覚えておきましょう。
Heteroskedasticityの影響を修正する方法
Heteroskedasticityの影響を修正する方法としては、White-corrected standard errorsを利用することが挙げられます。この修正後のstandard errorsを用いて検定を行うことで、より正しい検定を行うことが出来るようになります。
自己相関/時系列相関（Serial Correlation/Autocorrelation）
自己相関/時系列相関とは
回帰分析式の誤差項εに自己相関関係があることを自己相関/時系列相関があると言います。理想的には従属変数\(Y_t\)が独立変数\(X_t\)だけで説明されると良いのですが、誤差項\(ε_t\)が悪さをしてしまうわけです。
例えば、従属変数\(Y_t\)が一つ前の\(Y_{t-1}\)の結果に影響を受ける場合には独立変数\(X_t\)以外の誤差項に一つ前の結果が含まれて、従来の回帰分析式の予測力が大きく阻害されることになります。
以下は自己相関/時系列相関の例です。グラフを見てPositiveかNegativeかを問われることがありますので覚えておきましょうね。
出所：Schweser Notes自己相関/時系列相関の発見方法
回帰式の誤差項に自己相関があるかどうかを検定する際には、Durbin-Watson statistic(DW)という検定を行います。
ここでは、「誤差項に自己相関/系列相関が無いこと」が帰無仮説になります。
サンプルサイズが大きい場合、DW検定量は以下式で表現されます。rは自己相関係数です。
\[DW≒2(1-r)\]
DWは0から4の間の値を取ることが知られています。極端なケースで見ると、DWが0の時に正相関(r=1)、2の時に無相関(r=0)、4の時に負相関(r=-1)となります。
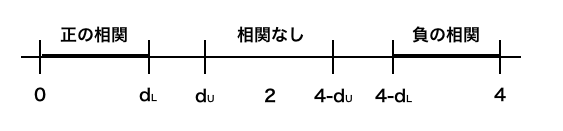
DWの検定では標本数に応じて、\(d_L\)と\(d_u\)が与えられ、DWと\(d_L\)と\(d_u\)の関係で相関有無が検定されます。
具体的には以下の図の太線のところにDWの数値が入れば棄却されることになり、それぞれ正の相関、負の相関がある（つまり、自己相関/系列相関がある）と言えることになります。
自己相関/時系列相関を直す方法
自己相関/時系列相関を直すにはHansen methodという方法が用いられます。ここではその方法の名前を覚えておきましょう。尚、Hansen methodはheteroskeasticityを直す効果もあります。
多重共線性(Multicollinearity)
多重共線性とは
独立変数(\(X_i\))相互の相関が強く表面的な決定係数\(R^2\)の値のみが増加する現象のことを言います。
例えば、重回帰分析に於いては一般に独立変数を増やせば増やすほど表面的な説明力（決定係数\(R^2\)）が増大しますが、複数の独立変数が同じ種類のもので相関関係が強い場合は、回帰分析の信頼性が揺らいでしまいます（通常、回帰分析では独立変数が少ない方が良いとされています）。
多重共線性の発見方法
決定係数やF値が大きい一方で各独立変数の係数のt値が低い場合、多重共線性を疑います。
多重共線性を直す方法
無駄な独立変数を除くため、独立変数の数を減らして再度確認をする等の手段が取られます。
定性的に表現される独立変数によるモデル
最後に以下の二つのモデルについて理解しておきましょう。さらっと問われる可能性があるので概要だけ掴んでおきましょう。
プロビット／ロジットモデル（Probit and logit models）
被従属変数が二者択一になる状況（例えば、デフォルト有無を判別する場合等）を表すのによく使われるモデルです。Probitモデルは正規分布を前提としていて、Logitモデルはロジスティック分布を前提としています。
判別モデル（Discriminant models）
Probitモデルやlogitモデルと似た概念ではありますが、線形直線で表されるのが特徴です。例えばスコアリング等でデフォルト率を判別するモデル等に利用されます。
