【QM】時系列分析（Time-Series Analysis）について

時系列分析：Time-Series Analysis

時系列分析では、独立変数をt(時刻)として、連続する期間内での従属変数(例：\(y_t\))の動きを観察します。今まで学んだ単回帰分析や重回帰分析のうち、独立変数がt(時刻)となるものの回帰モデルと考えて下さい。時系列分析の主なものとして、①Simple linear trend modelと②log-linear trend modelがあります。

単純直線トレンドモデル：Simple linear trend model

Simple linear trend modelは直線で表現されます。最も簡単な数式は以下になります。前セクションで学んだ単回帰モデルの独立変数がtに変わった形ですね。

\(
y_t = b_0 + b_1t + ε_t, 　t = 1,2,…, T
\)

\(y_t\)・・・時刻tにおける数値（従属変数）
\(b_0\)・・・切片(intercept)
\(b_1\)・・・傾き(slope coefficient)
\(ε_t\)・・・誤差項(error term)
\(t\)・・・時間（独立変数）

単回帰モデルと同様で、上の数式の係数（\(b_0\)や\(b_1\)）を推定する際には、最小二乗法（Ordinary least squares)を用いて行います。係数の検定方法も同じで、t値を用いたt検定を行います。グラフのイメージ図は以下の通りです。横軸が時間で縦軸が値になります。青色のグラフが実データで黒色のグラフが回帰分析の結果になります。

 

 

Log直線トレンドモデル：log-linear trend model

時系列データ群の内、時刻が進むと共に数値が指数関数的に上昇するグラフや一定の水準で逓減していくグラフの場合は、log-linear trend modelを用います。

先ず、指数関数的な動きをするグラフの数式ですが以下のように示されます。

\(y_t\) = e^{b_0+b_{1(t)}}

\(y_t\)・・・時刻tにおける数値（従属変数）
\(b_0\)・・・切片(intercept)
\(b_1\)・・・成長率（定数）
\(e\)・・・自然対数の底
\(t\)・・・時間（独立変数）

 

グラフをご覧頂くと分かるように時間が経てば経つほど回帰式と実際の数値が乖離していくのが予想されます（実測値は指数関数的に値が大きくなる一方で、回帰モデルは直線のためどんどんと乖離が大きくなっていく）。こういった場合、Linear Trend Modelでは説明力が低くなってしまうことが多いです。

そのため、指数関数的なグラフに対してはlogを取って回帰するとうまくいくケースが多いです。具体的には、上の数式の両辺に底をeとするlogを取って以下のような数式を利用して行います。

\[
ln(y_t) = b_0 + b_1t + ε_t
\]

 

いかがでしょうか。より、実測値と回帰式がフィットするようになったと思いませんか。

このように指数関数的なグラフを扱う際には、両辺を底がeとなるlogを取ることでより説明力が高い回帰を行うことが出来ることを覚えておきましょう。金融関連のデータを扱っているとこういうケースは多いです。

モデルの選択方法

実際に、どちらのモデルを利用するのが良いかを判断する際には、実際にグラフの上に実測値をプロットして判断します。上のグラフを見て頂くと一目瞭然のように、数値をプロットして確認するのがとても重要です。

Trend Modelの限界

Study Session 7 と 8で学習したように、残差項同士が相関を持つ場合は、自己相関/時系列相関（Serial Correlation/Autocorrelation）となり、正確な回帰式を導くことが出来ません。

そのため、時系列分析で自己相関/時系列相関が発生しTrend modelを用いるには限界がある場合には、次の項目以降で説明するAutoregressive model(ARモデル)を利用することになります。

尚、前セクションでも学習したように、自己相関/時系列相関を検知する際には、Durbin Watson statistic(DW)を用いる点を覚えて起きましょう。

ARモデル：Auto Regressive Modelsについて

Auto Regressive Models（ARモデル）とは、従属変数が自身の過去時点の値で説明されるような回帰モデルのことを言います。つまり、今時点の値が前の値に左右されるようなモデルです。具体的には以下のような数式で表現されます。

\(x_t = b_0 + b_1x_{t-1} + ε_t\)

\(x_t\)・・・時刻tにおける数値
\(b_0\)・・・切片(intercept)
\(b_1\)・・・傾き(slope coefficient)
\(x_{t-1}\)・・・時刻t-1における数値
\(ε_t\)・・・残差項
\(t\)・・・時間

ご覧いただくとわかるように、\(x_t\)は\(x_{t-1}\)の値に左右されます。

ちなみに、独立変数がpつあるもののARモデルをAR(p)と表現します。

AR(p)の数式は以下になります。

\[
x_t = b_0 + b_1x_{t-1} + b_2x_{t-2} + … + b_px_{t-p} + ε_t
\]

pが1の時は説明変数が一つになり、2の時は2つになります。

尚、AR(1)は以下のようにtの値をずらして示すことも出来ます。

時間がずれたとしても関係式は壊れません。

\[
\hat{x_{t+1}} = \hat{b_0} + \hat{b_1}x_t
\]

\[
\hat{x_{t+2}} = \hat{b_0} + \hat{b_1}x_{t+1}
\]

ARモデルの定常性について

ARモデルの係数の推定は、単回帰分析と同様、最小二乗法（Ordinary least squares:OLS）にて行いますが、ARモデルが正しく構築されるには（説明力ある回帰モデルとなるためには）、定常性（Covariance stationary）を満たす必要があります。一般的に以下の３つを満たす場合、定常性を満たすとされています。

定常性（Covariance stationary）とは、時間や位置によって確率分布が変化しないことを指し、期待値や分散、共分散も時間や位置によって変化しないことです。

1. 時系列データ群の期待値はどの時点でも常に一定
2. 時系列データ群の分散はどの時点でも常に一定
3. 時系列データ群の共分散はどの時点の値同士を見ても一定

尚、多くの経済データや金融データが常に定常性を示すわけではありません。対象とするデータの期間の長さや経済環境の状況によって、定常性の有無が変わることがある点は覚えておきましょう。

ARモデルの自己相関性について

ARモデルを正しく構築するためには、誤差項が自己相関性を示してはなりません（仮に誤差項が自己相関を示す場合には正しく構築されません）。ここら辺は単回帰分析の内容と同様です。

ARモデルが正しく構築されているかどうかを確認する際には、誤差項の自己相関値を計算して、帰無仮説（自己相関値=0）としてt検定で棄却出来ないことを確認します。つまり、自己相関値が有意に0以外の数とは言えないことを示します。

尚、今まで誤差項の自己相関性を検知する際にはDurbin Watson statistic(DW)を利用していましたが、ARモデルの場合はDWを使わずにt検定を利用することを忘れないでおきましょう。

ちなみに、t値は\(\frac{自己相関値}{\frac{1}{\sqrt{標本数}}}\)で計算されます。

以下のSchweserの問題(サンプル数:102)で説明すると、Lag2の自己相関値が有意に0以外の数であるとは言えないことを示すために、t値を計算して、t分布(両側検定, 信頼水準5%, 自由度n-2: 100)から棄却値(1.98)を確認し、t値の絶対値と比較します。

t値が棄却値よりも絶対値が大きければ棄却（自己相関値は有意に0では無い：自己相関性がある）となりARモデルは正しく構築されていないことが確認されます。

\(t = \frac{0.0843368}{\frac{1}{\sqrt{102}}} = 0.8518\)

→1.98よりも小さいため、棄却出来ず（Lag2は有意に自己相関性があるとは言えない）。

最終的に全てのLagで確認を行います。

 

ARモデルの平均回帰性（Mean-reverting）について

時系列モデルでは長期間で見ると平均に近づいていく場合、mean revertingであると言います。AR(1)では、mean reverting levelは\(\frac{b_0}{1-b_1}\)となります。詳しく見ていきましょう。

例えば、AR(1)の場合の数式は以下ですが、長期間経った時には一つの値（平均）に収束するので、\(x_t=x_{t-1}\)となります。つまり、数式は

\[
x_t = b_0 + b_1x_{t-1}
\]

ですが、\(x_t = x_{t-1}\)となるので、

\[
x_t = b_0 + b_1x_{t} \\
x_t(1-b_1) = b_0 \\
x_t = \frac{b_0}{1-b_1}\\
\]

よって、\(x_t\)が\(\frac{b_0}{1-b_1}\)よりも大きければ、\(\frac{b_0}{1-b_1}\)に収束するため、\(x_{t+1}\)は\(x_t\)よりも小さくなります。逆に、\(x_t\)が\(\frac{b_0}{1-b_1}\)よりも小さければ、\(x_{t+1}\)は\(x_t\)よりも大きくなります。

サンプル内予測（In-sample forecasts）とサンプル外予測（Out-of-sample forecasts）について

In-sample forecastsとは、モデルを推定する際に利用したサンプル内での予測になります。Out-of-sample forecastsとは、モデルを推定する際に利用したサンプル外での予測になります。特にOut-of-sample forecastsのモデルは将来予測をする上で重要です。

誤差項の二乗平均平方根について：Root Mean Squared Error criterion(RMSE)について

The root mean squared error criterion(RMSE)は、Out-of-sample forecastsのARモデルの精度を比較する際に利用します。2つのARモデル、AR(1)とAR(2)がある場合、RMSEが小さい方がより説明力が高いと言うことが出来ます。

ARモデルのランダムウォーク（Random Walk）について

ランダムウォーク（Random Walk）の時系列データは、とある時点の値が他の時点の値と残差項を足したものに等しいものを言う。数式は以下の通りです。

\[x_t = x_{t-1} + ε_t\]

ちなみに、上の数式に0以外の定数\(b_0\)を加えると、

\[x_t = b_0 + x_{t-1} + ε_t\]

となり、Random Walk with a Driftとなります。つまり、誤差項に加えて定数\(b_0\)も都度足されることになります。

ここでRandom WalkとRandom Walk with a Driftが定常性（Covariance Stationarity）を持つかどうかを調べます。

時系列モデルで定常性を持つ場合、Mean-reverting levelを持ちますが、Random WalkとRandom Walk with a Driftの場合、\(b_1=1\)とすると、\(\frac{b_0}{1-b_1}=\frac{b_0}{0}\)となり、数値を持ちません。そのため、Random WalkとRandom Walk with a Driftはmean reverting levelを持たず、定常性も持ちません。ちなみに、\(b_1=1\)の状態をunit rootと言います。

ARモデルの定常性を確認するテスト：Dickey Fuller test

ARモデルの定常性を確認するためには、前項で述べたような自己相関性を確認するためにt検定を行いますが、その他にunit rortが存在しないことを確認するテスト：Dickey Fuller testを行います。

Dickey Fuller testでは、AR(1)の数式の両辺から\(x_{t-1}\)を引いて、\(b_1-1\)が有意に0で無いことを示します。尚、この\(b_1-1\)をgと表現して、gが有意に0で無いことを確認をすることもありますが、言っていることは同じです。

\[
x_t = b_0 + b_1x_{t-1} + ε\\
x_t – x_{t-1} = b_0 + b_1x_{t-1} – x_{t-1} + ε\\
x_t – x_{t-1} = b_0 + (b_1 – 1)x_{t-1} + ε\\
\]

ARモデルの季節性（Seasonality）について

季節性(Seasonality)とは、時系列データ群が毎年同じような特性のパターンを示す場合に使われます（例：四半期の売上情報等）

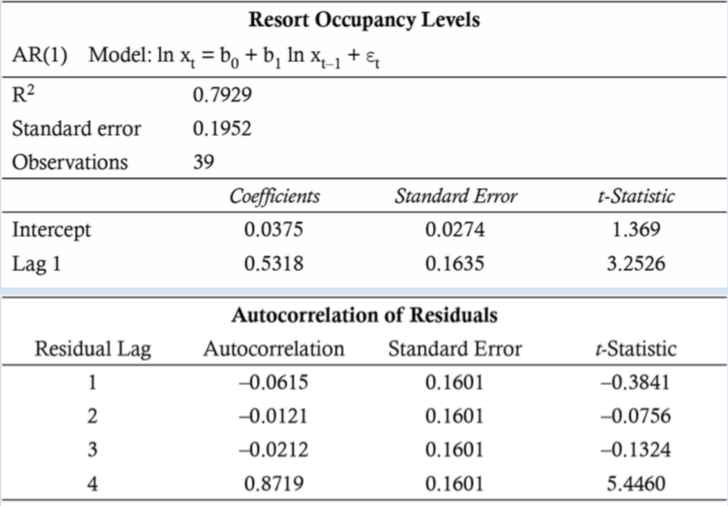
Seasonalityは他のARモデルと同様、誤差項の自己相関性を確認することで検知が可能です。例えば、以下のSchweserの事例を見てみましょう。

前の例で見たように、Autocorrelationの値を0として帰無仮説を置くと、例えばLag4のt値は\(t = \frac{0.8719}{0.1601} = 5.4460\)となり、両側t検定, 5%信頼水準, 自由度37(n-2)の棄却値は2.026であることから、t値が棄却値の絶対値よりも大きいため、Autocorrelationは有意に0では無いことが示されます。よって、このままでは正しくモデル化出来ていないことになります。（尚、Lag1〜3で確認するとt値は棄却されないことが確認できます）

 

そこで、モデルに新たな項を入れることを検討します。例えば、Lag4でエラーが発生しているので、\(lnx_{x-4}\)の項を追加します。その結果が以下の通りです。ARモデルが季節性を示す場合には、適切な項を追加することで正しいモデル化を行うことが可能となります。

 

上の表ではLag4のt値は-0.2610となっており、絶対値が棄却値の絶対値（2.026）よりも小さいので棄却されず、ARモデルに自己相関性は無いことが確認出来ました。

ARモデルが季節性を示す場合には、適切な項を追加することで正しいモデル化を行うことが可能となるわけです。

ARモデルの分散不均一性の検知方法：Auto Regressive Conditional Heteroskedasticity(ARCHモデル）

ARモデルの分散不均一性（ARCH）は、誤差項の分散が前期間の分散との間で相関を持つ場合に生じます。ARCHは以下式にて検知されます。

\[
\hat{ε_t^2} = a_0 + a_1\hat{ε_{t-1}^2} + μ_t
\]

この\(a_1\)が有意に0で無い場合にARCHが存在すると言え（\(a_1\)が0で無いと誤差項との間に関係が生じる）、その誤差の分散は以下数式にて予測することが出来ます。

\[
\hat{σ_{t+1}^2} = \hat{a_0} + \hat{a_1} + \hat{ε_t}^2
\]

二つの確率変数（\(x_t\),\(y_t\)）を用いる場合の回帰モデルの利用可否について

時系列解析を二つの確率変数\(x_t\)と\(y_t\)を用いて行う場合、まず、Dickey Fuller Testを行ってunit rootの有無を確認しますが、以下のようなパターンに分類されます。

1. 両方の時系列データ群は定常性を持つ。
2. 従属変数（\(y_t\)）のみが定常性を持つ。
3. 独立変数（\(x_t\)）のみが定常性を持つ。
4. 両方とも定常性を持たないし、両方の時系列データ群はCointegratedでは無い。
5. 両方とも定常性を持たないが、両方の時系列データ群はConintegratedである。

Cointegratedとは、両方の時系列データ群が同様の傾向を示しそれが時間を通じて変わらないことを言います。

一つ目は問題無く推定した回帰モデルを利用できますが、二つ目と三つ目の回帰モデルは定常性を持たないため利用できません。また、五つ目のように両方とも定常性を持たない場合でも、両方の時系列データ群がCointegratedの場合は、推定した回帰モデルを利用することが可能となる。そのため四つ目の回帰モデルは利用できません。

つまり、両方の時系列データ群が定常性を持つか、両方の時系列データ群が定常性を持たずにCointegratedの場合にその回帰モデルを利用可能と言うことです。

ちなみに、二つの時系列データ群がcointegratedかを判断する際には、Engle and Grangerによるt値を利用したDickey Fuller testが用いられる。これらのテストのことをDF-EG testと呼びますので覚えておきましょう。