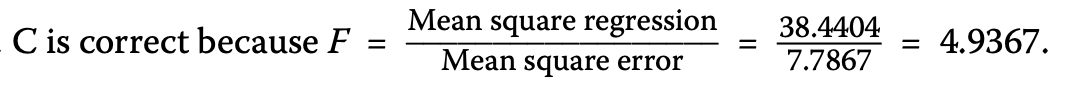CFA Level I Quantitative Methods の単回帰分析の導入で出てくるANOVA Tableはとても大事なので理解しておきましょう。
まず初めに以下のようなXとYの散布図に対して直線を引くケースを考えてみましょう。
ここでは、直線の式を
\[
\hat{Y}_i=\hat{b_0}+\hat{b_1}X_i
\]
としています。\(b_0\)(切片:intercept)、\(b_1\)(傾き:slope coefficient)です。
 出所:Schweser Notes
出所:Schweser Notes
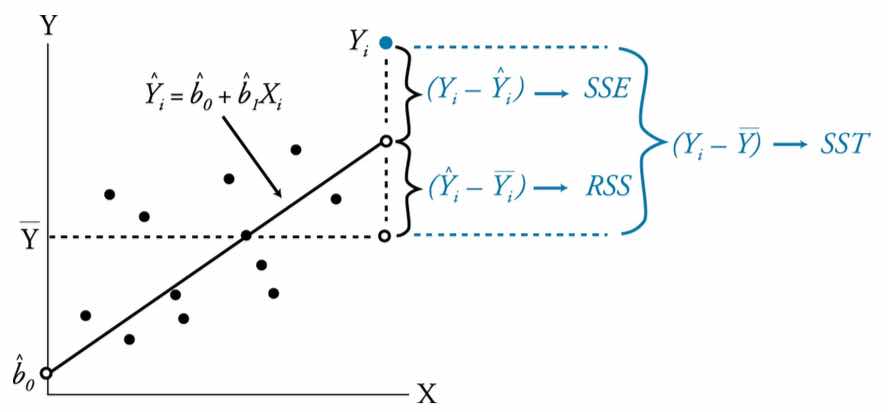
Yの実測値(実際に計測した値)を\(Y_i\) 、Yの実測値の平均値(実際に計測した値の平均値)を\(\bar{Y_i}\)、回帰分析で導き出した一次関数から算出したYを\(\hat{Y_i}\)とすると、それぞれの距離を二乗して足したものをSum of Square Error(SEE)、Regression Sum of Square(RSS)、Sum of Square Total(SST)と整理することが可能です。数式は以下の通りです。
Sum of Square Error(SSE):\(\Sigma(Y_i – \hat{Y_i}) \)
Regression Sum of Square(RSS):\(\Sigma(\hat{Y_i} – \overline{Y_i}) \)
Sum of Square Total(SST):\(\Sigma(Y_i – \hat{Y_i})+\Sigma(\hat{Y_i} -\overline{Y_i}) = \Sigma(Y_i – \overline{Y_i})\)
つまり、SSE + RSS = SST となります。
ちなみに、SSE + RSS = STTの両辺をSTTで割ると、(SSE/STT) + (RSS/STT) = 1となります。ここで、(RSS/STT)の事を決定係数と呼び\(R^2\)と表現します。
(RSS/STT) = 1 – (SSE/STT) で、SSE(回帰式と実測値の誤差)が小さければ小さいほど、回帰式の実測値に対する説明力が高いということになります。例えば、決定係数が0.8であれば回帰式が実測値の8割を説明することになります。
尚、決定係数はXとYの相関係数の二乗と等しいことが知られています。つまり、計算で決定係数を算出したらその平方根をとると相関係数が求められると言うことです。
また、この決定係数の特徴として独立変数の数が大きければ大きいほど表面的な説明力が増したように見えることがあります。こういった影響を排除するために、自由度調整後決定係数というもので測ることもあります。試験で単発で問われる可能性がありますので、以下数式を覚えて計算出来るようにしておきましょう。
\[
Adjusted R^2 = 1-[(\frac{n-1}{n-k-1})×(1-R^2)]
\]
それでは、最後にANOVA Tableについて見ていきましょう。ANOVA Tableは上での述べたような事を表にして分かりやすく纏めて、回帰式の妥当性検証を行いやすいように必要数値を一覧表にしたものになります。
| 要因 | 自由度(df) | 平方和 | 平均平方 | F値 |
| Regression | k(定数項以外の独立変数の数) | RSS | MSR =RSS / k |
F = MSR/MSE |
| Error | n-k-1 | SSE | MSE =SSE / n-k-1 |
|
| Total | n-1 | SST |
- 全体の自由度は、観察値(n)の数から1を引いたn – 1となります。
- kは定数項以外の独立変数の数です。単回帰分析の場合はk = 1となります。
- F値は大きければ大きい程、回帰式による説明力が大きい(誤差による説明力が小さい)という事を示します。十分に大きければモデルとして説明力があると言えます。
- 決定係数はRSS/SSTで求めることができ、これもモデルの説明力を示します。1に近い方が説明力が高いということになります。
- MSEの平方根を取ったものをSEE(Standard error of the estimate)と呼んでいます。これは実測値が回帰式から計算される推測値から平均的にどれぐらい乖離しているかを示しています。単発で計算する問題がありますので覚えておきましょう。
<練習問題1>
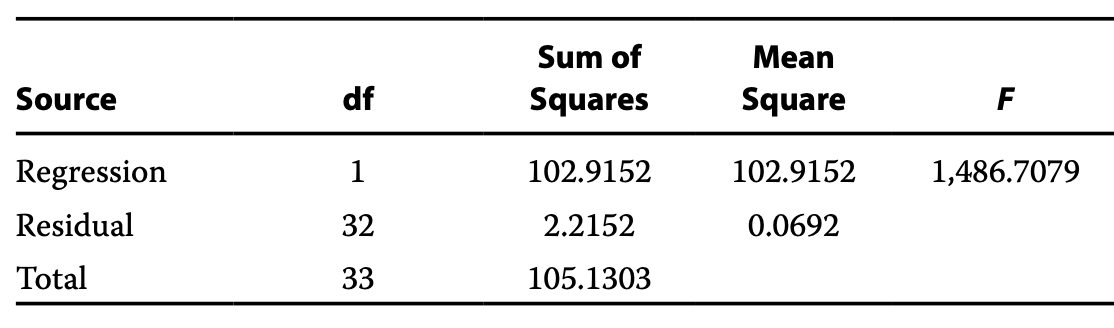

まずは決定係数の出し方ですね。公式通りです。
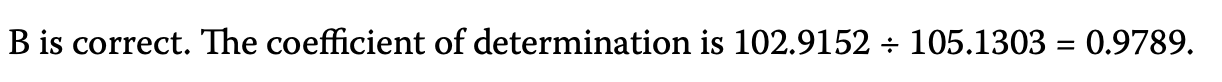

続いて標準誤差ですね。こちらも公式通りです。
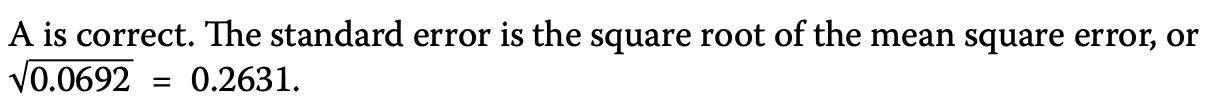
<練習問題2>


今度はF値を求める問題ですね。こちらも知っていれば瞬殺ですね。