【EC】通貨為替レート : 均衡価値の理解 (Currency Exchange Rates: Understanding Equilibrium Value)

Contents

通貨為替レート：均衡価値の理解（Currency Exchange Rates: Understanding Equilibrium Value）

通貨為替レート：均衡価値の理解（Currency Exchange Rates: Understanding Equilibrium Value）

外国為替建値（Forex Quotes）

直物為替レート(Spot exchange rate)とは、現時点で交換可能な通貨交換レートを指しています。約定されると、通常、取引日の2日後に取引が完了します。

先物為替レート(Forward exchange rate)とは、将来の特定日に交換するレートのことを指し、例えば、30日後、60日後、90日後、1年後等の将来に交換が行われます。

金融機関やディーラーは外国為替建値を「$1.4124(bid) – 1.4128(ask)」というように交換レートを提示します。この見方は覚えておきましょう！尚、askはofferとも呼ばれます。

BidとAskの違いについては確りと覚えておきましょう。

金融機関やディーラーが顧客から買う価格（レート）がbid

金融機関やディーラーが顧客に売る価格（レート）がask

先輩

建値の見方は基本中の基本なので確りと学びましょう！

スプレッド（Spreads）

Askとbidの差分のことをスプレッド（spread）と呼びます。数式は以下の通りです。

\[
Bid-Ask　spread　=　Ask　quote　-　Bid　quote
\]

例えば、先程の例では外国為替建値は「$1.4124(bid) – 1.4128(ask)」ですが、二つの差分の0.0004がスプレッドとなります。

ディーラーが提示するスプレッドは、①インターバンク市場のスプレッド、②取引サイズの大きさ、③ディーラーと顧客の関係度合いに依存して決定します。

インターバンク市場のスプレッドは、①通貨の種類や②時間帯、③マーケットのボラティリティ状況によって決定します。

先物為替レート（Forward exchange rate）のスプレッドである、Forward spreadsは、交換日の満期が長い程、大きな値になります。主な理由は、①期間が長いほど流動性が少なくなること、②金利リスクが大きくなること、そして、③取引相手の信用リスクが大きくなることです。

フォワード・プレミアム（Forward premium）とは、直物為替レート（Spot exchange rate）よりも先物為替レート（Forward exchange rate）の方が大きいことを指します。

フォワード・ディスカウント（Forward discount）とは、直物為替レート（Spot exchange rate）よりも先物為替レート（Forward exchange rate）の方が小さいことを指します。

例えば、スポットが1.20$/€でフォワードが1.25$/€の場合は、€は$に対してforward premiumと言います。逆に$は€に対してforward discountと言います。一つの取引でも基準とする通貨が異なれば表現が異なりますので気をつけましょう。

サイト運営者

基準とする通貨と交換相手の通貨の関係を見つつ、正確に情報を捉えるように訓練しよう！

三角裁定（Triangular Arbitrage）

三角裁定による収益計算方法を覚えておきましょう。三角裁定とは、三通貨間の為替裁定取引のことを指し、三ヶ国の通貨のbid askを用いて裁定収益を求める問題です。

例えば、インターバンク市場では以下のようなbid-askがあったとします。

$USD/AUD　0.6000 – 0.6015$

$USD/MXN　0.0933 – 0.0935$

$MXN/AUD　6.42 – 6.4481$

ここで、ディーラーから以下のようなbid-askを提示されたとします。

$MXN/AUD　6.3000 – 6.3025$

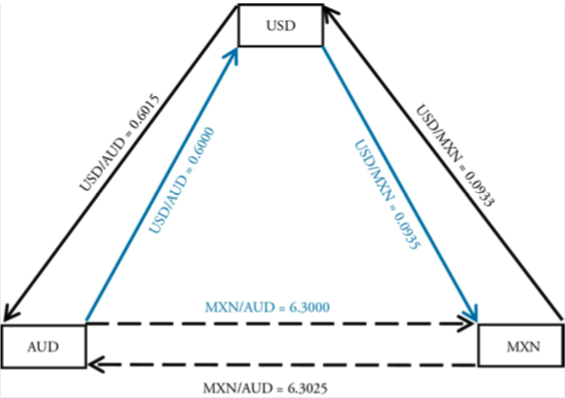
この時に、$1millを用いて裁定取引が可能かを考えます。図で整理すると以下のような関係になります。つまり、USD → MXN → AUD → USD として利益が出るかを確認します。

(USD)：$1mill → (MXN)：$\frac{$1mill}{0.0935}$ → (AUD)：$\frac{\frac{$1mill}{0.0935}}{6.3025}$ → (USD)：$\frac{\frac{$1mill}{0.0935}}{6.3025} × 0.6000=$$1.018185mill　つまり、$18,185を裁定取引で得ることが出来ます。

出所：Schweser Notes

このようにインターバンク市場とディーラーのレートをうまく組み合わせることで、裁定取引を行うことが出来ます。三角裁定は確りと勉強しておきましょう。

サイト運営者

三角裁定の問題は必ず解けるようにしておこう！

時価評価（Mark-To-Market Value）

先物為替取引の時点t (0 < t < T)の時価は以下の計算式で導かれます。

\[
V_t = \frac{(FP_t – FP)(contract size)}{1 + R(\frac{days}{360})}
\]

$V_t$・・・時点tの先物為替取引の時価
$FP$・・・約定した先物為替レート（満期T）
$FP_t$・・・時点tの先物為替レート（満期T）
$days$・・・時点tから満期Tまでの日数
$R$・・・価格表示通貨の金利

この数式は、時点tに新たに同様の取引を約定したと仮定して、満期Tにおいて最初に約定した取引と時点tで約定した取引の差額を計算して、それを時点tまで金利で現在価値に割り戻したものと言えます。

サイト運営者

先物為替レートの時価を求める問題は単発で聞かれる可能性があるので準備しておこう！

為替決定理論：国際パリティ関係（Parity Conditions）

ここでは為替に関する国際パリティの関係式を覚えておきましょう。先ず、覚えておくべき関係図は以下の通りです。この表を自分で導けるようになるまで、がっちり勉強しましょう！逆にこの関係式を真っさらな用紙の上に何も見ずに書いて説明出来るようになれば、完璧です！

出所：Schweser Notesを参考に当サイト運営者作成

サイト運営者

上の関係式を説明するそれぞれの項目を見ていきましょう！

先物為替レート平価（Forward Rate Parity）

将来の直物為替レート予想値($E(S_t)$)と先物為替レート$(F)$が一致する場合、「Forward Rate Parity」が成立すると言います。上の図の左側の関係です。

カバー有り金利平価（Covered Interest Rate Parity）

先物為替レート($F$)は両通貨の金利格差で説明されるというもので、現在の直物為替レート($S_0$)に両通貨の金利調整を行って計算されます。計算式は以下の通りです。

$
F=\frac{1+R_A}{1+R_B}S_0
$
$F$・・・先物為替レート（通貨A/通貨Bで表示）
$S_0$・・・直物為替レート（通貨A/通貨Bで表示）
$R_A$・・・通貨Aの金利
$R_B$・・・通貨Bの金利

カバー無し金利平価（Uncovered Interest Rate Parity）

将来の直物為替レート予想値($E(S_t)$)は、為替の変動は両通貨の金利格差で説明がされるというもので、現在の直物為替レート($S_0$)に両通貨の金利調整を行って計算されまる。計算式は以下の通りです。

$
E(S_t)=\frac{1+R_A}{1+R_B}S_0
$
$E(S_t)$・・・将来の直物為替レート予想値（通貨A/通貨Bで表示）
$S_0$・・・直物為替レート（通貨A/通貨Bで表示）
$R_A$・・・通貨Aの金利
$R_B$・・・通貨Bの金利

サイト運営者

カバー有り金利平価の数式と同じですね！

あなた

違いは何になるのでしょうか・・・？

サイト運営者

対象としているのが、先物為替レートなのか将来の直物為替レート予想値なのかの違いです。この二つは似ているけど違う概念なので気をつけて下さい！先物為替レート平価（Forward Rate Parity）が成立する時に二つは同じになります！

ちなみに先程の数式、$E(S_t)=\frac{1+R_A}{1+R_B}S_0$を変形すると、$\frac{E(S_t)}{S_0}=\frac{1+R_A}{1+R_B}$（式１）となりますね。ここで、$\frac{E(S_t)-S_0}{S_0}$（式２）をμとすると、$μ=\frac{E(S_t)-S_0}{S_0}$で、$\frac{E(S_t)}{S_0}=1+μ$となります。これを（式１）に代入すると、$1+μ=\frac{1+R_A}{1+R_B}$で、さらに展開すると、$1+R_B+μ+μR_B=1+R_A$となり、$μ=R_A-R_B+μR_B$です。$μR_B$は小さい数なので無視すると、$μ=R_A-R_B$となり、（式２）に戻すと、以下の式が成立します。

\[\frac{E(S_t)-S_0}{S_0}=R_A-R_B\]

実際の問題を解く際にはこの近似式を用いて計算することがあるので、覚えておきましょう！

勉強仲間(男)

Schweserを読んでも良く分からなかったんだよね。助かります！

国際フィッシャー関係式（International Fisher Relation）

国際フィッシャー関係式とは自国と外国の名目金利の差は期待インフレ率の差を表しているとするものです。
実質金利は国を超えて等しいはずという考えで、それゆえ金利差がインフレ率格差を反映すると考えます。数式は以下の通りです。

$R_{nominal A} – R_{nominal B} = E(inflation_A) – E(inflation_B)$
$R_{nominal A}$・・・A国の名目金利
$R_{nominal B}$・・・B国の名目金利
$E(inflation_A)$・・・A国の期待インフレ率
$E(inflation_B)$・・・B国の期待インフレ率

相対的購買力平価（Relative PPP）

相対的購買力平価では、二国間のインフレ率の差が為替先物を決定すると考えます。要は、高インフレ率の国の為替は減価していくはずだということです。数式で表現すると以下の通りです。

$F=\frac{E(inflation_A)}{E(inflation_B)}S_0$
$F$・・・先物為替レート
$S_0$・・・直物為替レート
$E(inflation_A)$・・・A国の期待インフレ率
$E(inflation_B)$・・・B国の期待インフレ率

相対的購買力平価は、長期的に見れば為替は次第に購買力平価レベルに収束していく傾向がありますが、短期的には当てはまらないという点は覚えておきましょう！（問われることがあります！）

サイト運営者

ここまで理解したらもう一度国際パリティ関係を見てみよう！きっと、今まで以上に理解が進むはずです！

上司

国際パリティ関係を真っさらな用紙にゼロから書いて説明出来るようになれば完璧ですね。

FX キャリードレード（Carry Trade）

FXキャリー取引では、低いイールドの通貨を借りて、高いイールドの通貨に投資します。

FXキャリー取引の収益(Profit on carry trade) = 金利差(interest differential) − 投資通貨の為替変化(change in the spot rate of the investment currency)となります。つまり金利の収益と為替の収益のネットです。

FXキャリー取引は、先程説明したカバー無し金利平価（Uncovered interest rate parity）が成立していないことを前提に行います（仮に成立していると仮定すると、金利差額分だけ投資した通貨が減価するため出来上がりトントンになる）。

FXキャリー取引は、借入した通貨が想定以上に強くなる場合(Appreciation)、損失が膨らむ可能性があります。例えば、マーケットが荒れている時(ボラティリティが高い時)等はFXキャリー取引は止めるべきでしょう。

尚、マーケット参加者は同じようなことを考えるので、ネガティブな事象が発生した際に、FXキャリー取引の多くが同時に取引を停止することで為替が大きく動くことがあります。これをクラッシュリスクと呼びます。

国際収支統計が為替に与える影響（Balance of Payment: BOP Influence on exchange）

国際収支(BOP)統計とは、一定の期間における居住者と非居住者の間で行われたあらゆる対外経済取引（財貨、サービス、証券等の各種経済金融取引、それらに伴って生じる決済資金の流れ等）を体系的に記録したものです。

この国際収支が為替に与える影響は、経常収支(Current Account)による影響と資本収支(Capital Account)による影響をベースに分析されます。尚、資本収支は金融収支(Financial Account)とも言います。

経常収支とは、国内居住者と外国人（非居住者）との間のモノ（財貨）・サービスの取引（輸出入）、対外金融債権・債務から生じる利子・配当金等の収支、居住者と非居住者との間の対価を伴わない資産の提供に係る収支等で構成されます。

経常収支が赤字になると自国通貨は減価（depreciation）すると言われています。それらのメカニズムは以下3つで説明されます。

Flow supply/demand mechanism.経常収支の赤字（つまり輸入超）は、対外国が得た自国通貨を対外国通貨に変える圧力が高まるため、自国通貨が減価する動きとなります。
Portfolio composition mechanism.経常収支で得た黒字部分は資本収支の投資等に充当されますが、投資国では対外国通貨の資産が増えます。この投資国がその資産を自国通貨に変えることで、投資される側の国の通貨は減価します。
Debt sustainability mechanism.経常収支が赤字の国は、対外国からの借入によって赤字を賄います。GDP対比高い負債比率となる場合は投資家がその返済能力に疑問を持ち、当該国の通貨を買わなくなりその通貨は減価します。

資本収支とは、直接投資、証券投資、金融派生商品、その他投資及び外貨準備の合計のことを指し、金融資産にかかる居住者と非居住者間の債権・債務の移動を伴う取引の収支を表します。

資本収支の流入（流出）は為替レートの増加（低下）を引き起こす大きな理由の一つと言われています。資本が当該国に流れ込むことで当該国通貨の需要が高まり、その通貨の価値は強くなります（Appreciation）。通常、新興国等のインフレ調整後の収益が高い国（成長率が高い国）に資本が集まりますが過度な資本流入は悪影響を及ぼします。例えば、過度な対外借入の増加やバブルの発生等が挙げられます。新興国政府はこういった影響を防ぐために、直接投資に制限をかけたり為替介入等を行なっています。

金融政策と財政政策

マンデルフレミングモデル（Mundell-Fleming model）

マンデルフレミングモデルは、金融政策と財政政策が金利に与える影響を評価し、結果として為替に与える影響を評価します。インフレ率変化の影響は無視をしています。短期的な影響を見ており長期的には利用出来ません。ここでは以下の金融政策と財政政策が為替に与える影響の表を覚えておきましょう。

金融政策	財政政策	資本移動制限無し	資本移動制限有り
拡大	拡大	Uncertain	Depreciation
拡大	緊縮	Depreciation	Uncertain
緊縮	拡大	Appreciation	Uncertain
緊縮	緊縮	Uncertain	Appreciation

ここでは特に資本移動に制限が無い場合の通貨影響を覚えておきましょう（上の太字箇所）。

＜金融政策：拡大、財政政策：緊縮＞

金融政策を拡大する場合は、政策金利が低くなるので金利低下の動きとなります。また、財政政策の緊縮は財政赤字が縮小して国の信用力が高まるので金利低下の動き。結果として、全体的に金利は低下し、当該国の通貨は投資対象として魅力が減るので売られ減価（Depreciation）することになります。

＜金融政策：緊縮、財政政策：拡大＞

金融政策を緊縮する場合は、政策金利が高くなるので金利上昇の動き。財政政策の拡大は財政赤字が増加して国の信用力が低下するので金利上昇の動き。結果として、全体的に金利は上昇し、当該国の通貨は投資対象として魅力が高まるので買われ価値が高まる（Appreciation）ことになります。

金融政策による影響を確認するモデル（Monetary Model）

このモデルでは、金融政策のみを加味した場合の為替影響を分析します。マンデルフレミングモデルでは、インフレ率を考慮していませんでしたがこのモデルでは加味されることになります。

Pure monetary model

購買力平価が成り立つと仮定し生産は一定とします。金融緩和によりインフレ率が高まると物価が上昇し結果として自国通貨が減価します。ここでは将来の金融政策影響は無視します。

サイト運営者

下の相対的購買力平価の数式を見れば一目瞭然ですね！

Dornbusch overshooting model

このモデルでは、短期的には金融政策の影響を受けた為替の動きとなりますが、長期的には購買力平価で想定される為替レートに近づくとしています。例えば、金融緩和を行うと金利が下がり、自国通貨の魅力が下がるので通貨は減価することになりますが、次第に購買力平価で想定される為替レートに近付いて行くというものです。

財政政策による影響（Portfolio balance approach）

このアプローチでは、財政政策だけを加味して為替影響を判断します。マンデルフレミングモデルでは、短期的な財政政策の影響を見ていましたが、このアプローチでは長期的な視点で見ていきます。財政赤字の場合、政府は投資家から借入をしますが、この投資家は国家の財政状況を見て投資有無を決めます。ある程度のところまでは財政拡大すればリターンが高まるため投資の魅力が高まりますが、一定程度以上の財政拡大を行うと赤字が大きくなり投資の魅力が低まり、資金の引き上げが始まります。すると、為替が減価することになります。逆も然りです。