Contents
経済成長（Economics Growth）
この項目では、国家の経済成長に関する内容を学習します。各種前提や成長率が上昇する条件、経済成長のドライバー等を理解します。それでは内容を見ていきましょう！
経済成長要因と生産関数：Growth Factors And Production Function
経済成長要因
経済が成長する要因としては例えば以下の項目が挙げられます。
- 高い貯蓄率と投資（Savings and investment）
- 金融市場の仲介機能がうまくワークしていること（Financial markets and intermediaries）
- 政治的な安定（Political stability）
- 法制面/権利面の安定（Rule of law, property rights)
- 人的資本への投資：教育や訓練（Investment in human capital）
- 魅力的な税制や規制システム（Tax and regulatory systems）
- 自由貿易と自由な資本移動（Free trade and unrestricted capital flows）
- 技術進歩（Technology）
生産関数(GDPの計算)
GDPを計算するために利用する、ゴブ=ダグラス型生産関数（Cobb-Douglas production function）は覚えておきましょう。数式は以下の通りです。
\(Y = TK^αL^{1-α}\)
\(α\)・・・GDPに対する資本：capital(\(K\))の割合
\(1-α\)・・・GDPに対する労働力：labor(\(L\))の割合
\(T\)・・・全要素生産性（技術革新や教育・訓練による労働力の質の向上等）の影響
この数式の両辺をLで割ると、
\(\frac{Y}{L} = T(\frac{K}{L}^α)\)となります。これは、Lとαが一定だとすると、Tと\(\frac{K}{L})\)が高まる程、GDPが高まると言えます。尚、\(\frac{K}{L})\)のことを、Capital per worker(Capital Deepening)と言います。
つまり、技術革新や教育・訓練による労働力の質の向上、Capital Deepeningが大きい程、GDPが高まると言えます。
但し、αは1よりも小さい値を取るため、Capital Deepeningを大きくし続けたとしても、段々とGDPの増加効果は逓減していきます。成熟マーケットではCapital Deepeningによる効果が限定的なのはこれが理由です。これを打開するのが技術革新等の全要素生産性の効果です。以下のグラフで示されるように、全要素生産性の効果によりグラフが上にシフトすることでGDPが高まることになります。これらの関係をグラフを用いながら理解しておきましょう。
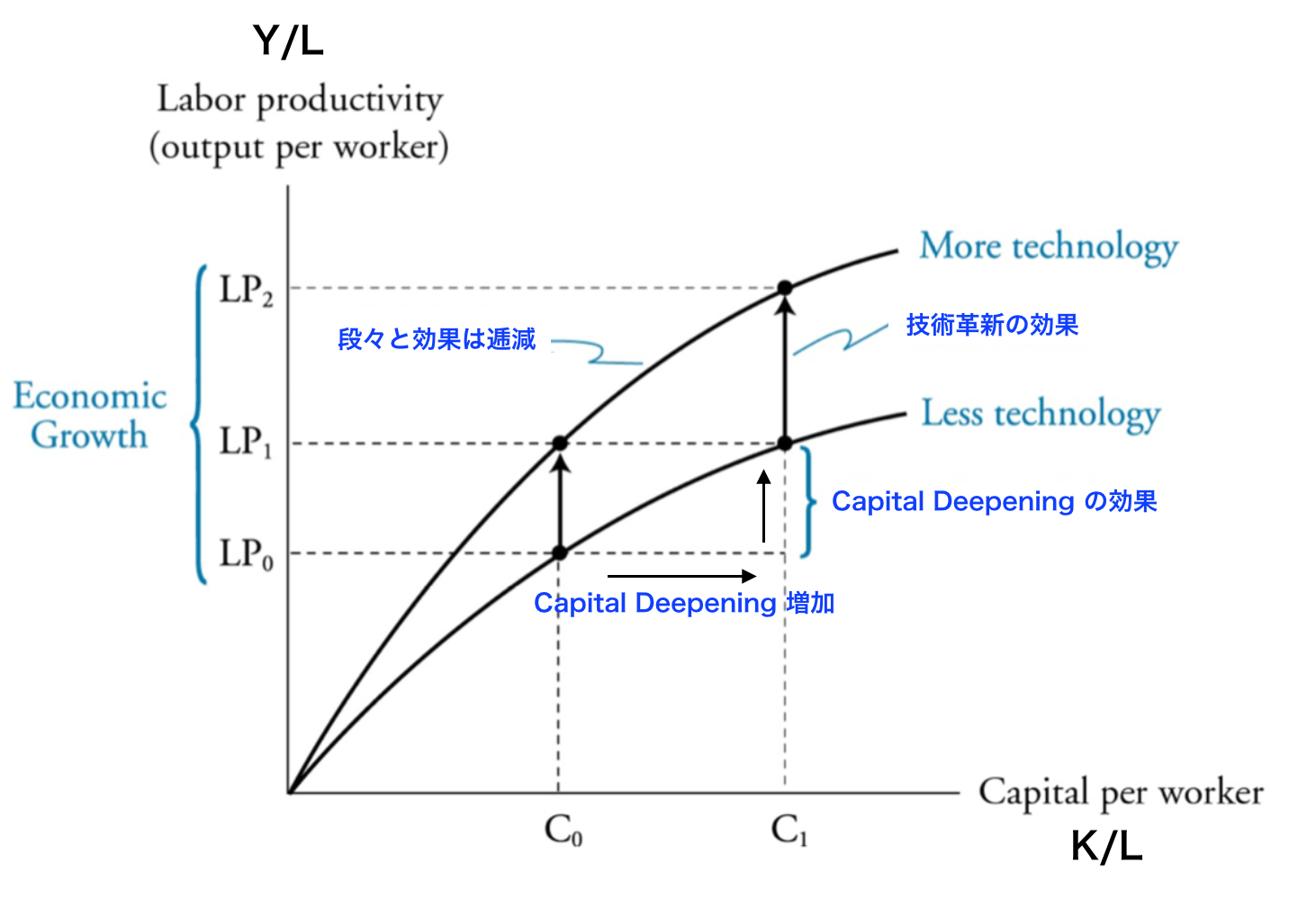出所：Schweser Notesを参考にサイト運営者作成成長会計と影響を与える要因：Growth Accounting And Influencing Factors
成長会計式（Growth Accounting）
成長会計式は以下の通りです。
\(\frac{ΔY}{Y}=α\frac{ΔK}{K}+(1-α)\frac{ΔL}{L}+\frac{ΔA}{A}\)
\(\frac{ΔY}{Y}\)・・・GDP成長率
\(\frac{ΔK}{K}\)・・・資本成長率
\(α\)・・・資本配分率
\(\frac{ΔL}{L}\)・・・労働力成長率
\(1-α\)・・・労働力分配率
\(\frac{ΔA}{A}\)・・・全要素生産性成長率（ソローの残差とも呼ばれます）
尚、資本配分率+労働配分率=1
貯蓄・投資により資本財蓄積が増加すれば労働者一人当たりの生産性が向上し生産性が増加します。また、労働力・労働時間が増加すれば生産は増加します。そして、研究開発費増加に伴う技術革新や、教育・訓練による労働力の質と向上、資源配分の効率性向上等で全体の生産効率が上がれば生産は増加します。
影響を与える要因： Influencing Factors
資源が成長に与える影響としてオランダ病（Dutch Disease）は覚えておきましょう。オランダ病とは、資源の輸出拡大で自国通貨が強くなり（Appreciation）、輸出競争力が弱まることから国内製造業を衰退させる現象です。外貨収入が急増して、一時的に好況を呈しますが、自国通貨の高騰や労働者賃金の上昇を招き、製造業の国際競争力が低下、経済が悪化し、失業率が高まります。
成長と収斂理論：Growth And Convergence Theories
新古典派成長論（Neo-Classical Growth Theory）
新古典派成長論では、長期的に見た安定的な経済成長率に焦点を当てます。労働力一人当たりGDPの継続的な成長率は、技術の成長率\(θ\)と労働力分配率\(1-α\)を利用して、以下数式で説明出来るとしています。
\(g^*=\frac{θ}{1-α}\)
全体の継続的な成長率は、上の数式に労働力成長率を足すことで算出出来るとしています。以下数式の通りです。
\(G^*=\frac{θ}{1-α}+ΔL\)
これら数式の通り、長期的に見た安定的な経済成長率は資本(K)に左右されないことがわかります。つまり、一度安定局面に入るとCapital DeepeningはGDP成長率に影響を与えません（注意：GDP自体の額には影響を与えます）。
Capital Deepeningは、短期的には影響を与えますが、長期的にはGDP成長率に影響を与えません。そのため、技術革新等によるシフトが無ければ、Capital deepeningを増加させたとしても、最終的には一定の成長率に収斂します。新興国であればCapital deepening増加に伴う逓減効果は小さいのでCapital deepening増加に伴うGDP成長率は大きくなります。尚、一般的に貯蓄が大きいほど投資可能額(K)は大きくなるので、GDPは大きくなります。
内生的成長理論（Endogenous growth theory）
新古典派の成長理論が技術進歩を外生的な所与のものとしているのに対し、内生的成長理論では技術進歩の発生の源泉を研究開発投資や人的資本の蓄積（教育水準や技能）に求めています。この理論では、①資本の限界生産額は一定で逓減しない、②貯蓄率の増加が一人当たり生産額の長期的な成長率を引き上げる としています。
資本の限界生産力は一定で逓減せず、Capital deepeningが大きくなっても一人当たりGDP率が低下しないとしています。
